Números arábigos curiosidad

El juego del ajedrez

Jugar al ajedrez tiene muchos beneficios. Aquí tienes un vídeo para empezar a practicar.

FIGURAS PLANAS

La idea de que el área es la medida que proporciona el tamaño de la región encerrada en una figura geométrica proviene de la antigüedad. En el Antiguo Egipto, tras la crecida anual de río Nilo inundando los campos, surge necesidad de calcular el área de cada parcela agrícola para restablecer sus límites; para solventar eso, los egipcios inventaron la geometría, según Heródoto.Leer más

Figuras planas y espaciales ANAYA
Polígonos JUNTA DE EXTREMADURA
lA CIRCUNFERENCIA Y EL NÚMERO PI INTERACTIVO
Medida de longitud INTERACTIVO
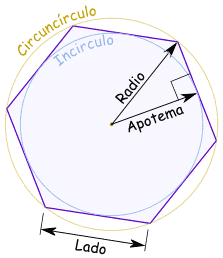Cálculo de longitudes, perímetros y distancias INTERACTIVO
La superficie INTERACTIVO
Cálculo de superficies INTERACTIVO
Áreas y perímetros ANAYA
Äreas INTERACTIVO
Cálculo de figuras planas DESCARTES
El juego de las formas INTERACTIVO
Deducción lógica de las fórmulas del área
Perímetros y áreas wikipedia

Algebra

Igualdad y ecuaciones (Genmagic)

El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). Es una de las principales ramas de la matemática, junto a la geometría, el análisis matemático, la combinatoria y la teoría de números.

Etimológicamente, la palabra «álgebra» جبر (yabr) , proviene del árabe y significa "reducción".(leer más)

Actividades algebra
1. Introducción al algebra
2. Lenguaje algebraico
3. Valor numérico monomios
4. Monomios semejantes
5. Ecuaciones con balanzas
6. Practicar con ecuaciones
7.Resolver ecuaciones
8. Problemas ecuaciones

• ANAYA interactiva
• Tema completo ED@D
• Resuelve problemas

Proporcionalidad

Llamamos magnitud a cualquier cualidad de los objetos que puede ser medida, como el peso, la altura, el tiempo, la velocidad...

En ocasiones se pueden establecer entre las magnitudes relaciones que nos permiten resolver problemas. Estas relaciones pueden resolverse mediante la proporcionalidad. Existen dos tipos de proporcionalidad: directa e inversa.

La proporcionalidad directa está basada simplemente en el producto muchos la hemos utilizado por ejemplo a la hora de comprar o de preparar una receta de cocina para un número distinto de personas. Eso hace que nos resulte muy sencilla de aplicar: si vamos a preparar un pastel para el doble de personas, tendremos que poner el doble de harina.

Las magnitudes también pueden ser inversamente proporcionales: si viajamos al doble de velocidad tardaremos la mitad de tiempo en llegar a nuestro destino.

Pero no todas las magnitudes son proporcionales y por eso tenemos que poner especial cuidado en no aplicar las reglas de la proporcionalidad sin pensar antes si existe relación entre las magnitudes del problema y, en caso de existir, si es de proporcionalidad directa, de proporcionalidad inversa o de otro tipo.

Proporcionalidad y porcentajes -Gobierno de Canarias

Temas clave:

                    Proporcionalidad

                      La proporción

Para practicar:

           ANAYA interactiva 1ºESO

           Aplicacionesinfo proporcionalidad

           Educatex Junta de Extremadura proporciones porcentajes
           Genmagic porcentajes
           Amolasmates proporcionalidad y porcentajes 
           Santillana 1º ESO

LAS ABEJAS SABEN CONTAR, PERO SOLO HASTA CUATRO

Científicos alemanes y australianos aseguran que tienen capacidad matemática y la misma habilidad que un chimpancé para distinguir objetos, algo que utilizan a diario para orientarse con edificios, árboles u otros objetos que haya en torno a su panal

Las abejas tienen capacidad matemática y saben contar, aunque sólo pueden hacerlo hasta cuatro, según un estudio realizado por científicos alemanes de la Universidad de Würzburg, integrados en el equipo internacional de trabajo BEEgroup.

El estudio, que publica la revista digital especializada PLoS One, afirma que las abejas tienen la misma habilidad que un chimpancé a la hora de distinguir objetos, aunque si se trata de contarlos no van más allá de cuatro.

El equipo de científicos alemanes, junto a varios colegas australianos, han conseguido por primera vez definir la capacidad de contar de un animal invertebrado. Para ello y durante dos años, los investigadores hicieron que la abejas de un panal volaran sistemáticamente a través de tubos de metacrilato con varias salidas.

Directamente en la abertura de los tubos, al igual que en las diferentes salidas, pintaron distintos objetos, como tres limones o cuatro hojas, para indicar a las abejas el camino a elegir a la hora de buscar alimento.

"Lo importante es la cantidad"

Con independencia del objeto dibujado, las abejas aprendieron, por ejemplo, que si a la entrada del tubo había tres objetos dibujados, debían buscar el tubo de salida con otros tres dibujos. Los científicos comprobaron que a la abeja le da igual el objeto dibujado -una estrella, una hoja, un limón o simples puntos- y que para orientarse se fijan en su cantidad, incluso cuando el objeto es completamente nuevo y desconocido.

"Las abejas no se dejan distraer por el objeto dibujado, sino que saben que lo importante es su cantidad", explican los científicos en el estudio, en el que subrayan que, a partir de cuatro o más objetos las abejas ya no saben contar.

Una capacidad innata

El estudio destaca que durante los experimentos realizados, las abejas acertaron en más del 70% de los casos con cuatro o menos objetos orientativos dibujados en las entradas y salidas de los tubos de metacrilato a la hora de buscar su alimento.

Se trata, según afirman, de una capacidad innata de los animales y el ser humano que no se aprende. Mientras el ser humano puede reconocer simultáneamente hasta cuatro objetos sin contarlos, la abeja tiene esa capacidad limitada a tres. A partir de cuatro objetos, la abeja ve "muchas" cosas, pero no es capaz de distinguir si se trata de cuatro, cinco o más.

Los responsables del experimento señalan finalmente que las abejas utilizan a diario su capacidad de contar para orientarse con edificios, árboles u otros objetos en el área en la que vuelan habitualmente en torno a su panal.

LAS FRACCIONES

Los egipcios en el siglo XVII a.C. manejaban las fracciones de forma muy curiosa: solamente como sumas de fracciones unitarias, es decir sumas de los inversos de los números enteros positivos, a excepción de 2/3 y 3/4. El jeroglífico que indicaba una fracción era una boca, y significaba "parte":

Las fracciones eran escritas con el signo r encima del número; en notación actual: 1 como numerador, y el otro escrito debajo como denominador. Así 1/3 se representaba como:

Había símbolos especiales para el 1/2 y para dos fracciones, 2/3 (usado con frecuencia) y 3/4 (utilizado algo menos):

Si el denominador era demasiado grande, la "boca" era puesta al principio del "denominador":

CONCEPTO DE FRACCION:

Jose Antonio cuadrado

El concepto matemático de fracción corresponde a la idea intuitiva de dividir una totalidad en partes iguales, como cuando hablamos, por ejemplo, de un cuarto de hora, de la mitad de un pastel, o de las dos terceras partes de un depósito de gasolina. Tres cuartos de hora no son, evidentemente, la misma cosa que las tres cuartas partes de un pastel, pero se “calculan” de la misma manera: dividiendo la totalidad (una hora, o el pastel) en cuatro partes iguales y tomando luego tres de esas partes. Por esta razón, en ambos casos, se habla de dividir dicha unidad (una hora, un pastel, etc.) en 4 partes iguales y tomar luego 3 de dichas partes. 

Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.

La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.


Actividades:
        Las fracciones
        Anaya
CONTENIDOS DIGITALES DE LA JUNTA DE EXTREMADURA    
       Problemas con fracciones.Introducción.
       Problemas con fracciones. Fracción como parte de la unidad.       Problemas con fracciones. Fracción como cociente de dos números.
       Problemas con fracciones. Fracción como operador.
        Fracciones y números decimales autoevaluación
Gobierno de Canarias:
       Multiplicación de fracciones
       División de fracciones
Educamadrid:
Fracciones